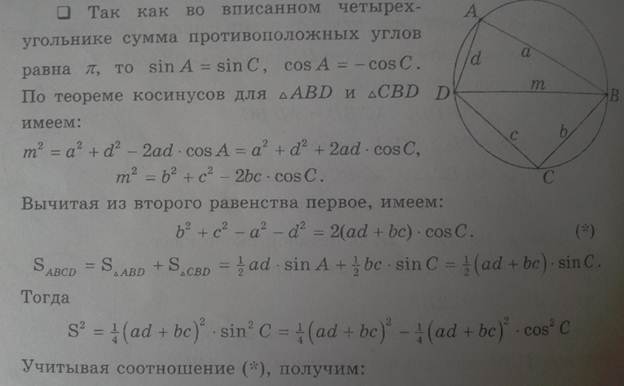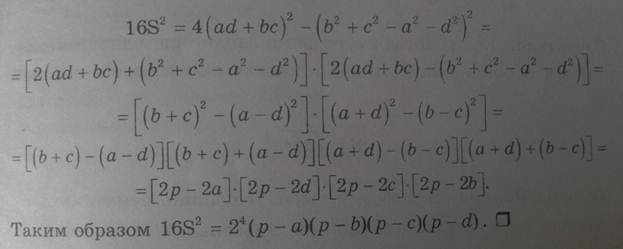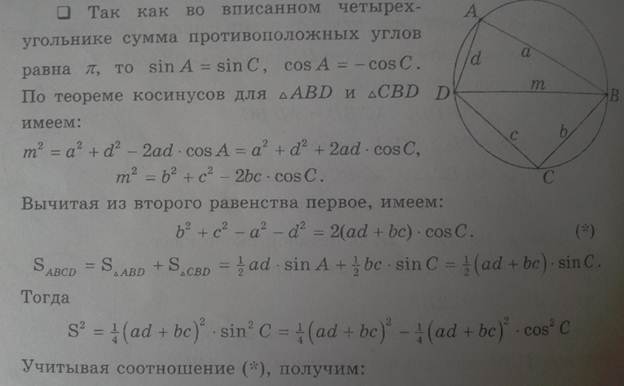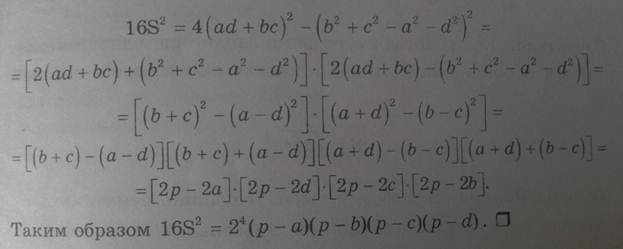Четырёхугольник — это геометрическая фигура (многоугольник), состоящая из четырёх точек (вершин), никакие три из которых не лежат на одной прямой, и четырёх отрезков (сторон), попарно соединяющих эти точки. Различают выпуклые и невыпуклые  и звездчатые четырёхугольники. Выпуклым четырехугольником называется четырехугольник, у которого все углы меньше развернутого угла. Четырехугольник, у которого угол больше развернутого называется невыпуклым

Виды четырёхугольников

Параллелограмм — четырёхугольник, у которого все противоположные стороны попарно равны и параллельны;
Прямоугольник — четырёхугольник, у которого все углы прямые;
Ромб — четырёхугольник, у которого все стороны равны;
Квадрат — четырёхугольник, у которого все углы прямые и все стороны равны;
Трапеция — четырёхугольник, у которого две противоположные стороны параллельны;
(Дельтоид — четырёхугольник, у которого две пары смежных сторон равны.)

Свойства

• Сумма углов четырёхугольника равна 2 π = 360°.
• Четырёхугольник можно вписать в окружность тогда и только тогда, когда сумма противоположных углов равна 180° (). См. также теорема Птолемея.
• Четырёхугольник является описанным около окружности тогда и только тогда, когда суммы длин противоположных сторон равны ()
• Формула Эйлера: учетверённый квадрат расстояния между серединами диагоналей равен сумме квадратов сторон четырёхугольника минус сумму квадратов его диагоналей.
• Средние линии четырёхугольника и отрезок, соединяющий середины его диагоналей, пересекаются в одной точке и делятся ею пополам.
• Четыре отрезка, каждый из которых соединяет вершину четырёхугольника с центроидом треугольника, образованного оставшимися тремя вершинами, пересекаются в центроиде четырёхугольника и делятся им в отношении 3:1, считая от вершин.
• Две противоположные стороны четырёхугольника перпендикулярны тогда и только тогда, когда сумма квадратов двух других противоположных сторон равна сумме квадратов диагоналей.
• Диагонали четырёхугольника перпендикулярны тогда и только тогда, когда суммы квадратов противоположных сторон равны.
• Средние линии четырёхугольника равны тогда и только тогда, когда равны суммы квадратов его противоположных сторон.

Теорема Вариньона
Четырёхугольник, вершины которого совпадают с серединами сторон произвольного четырёхугольника, является параллелограммом, стороны которого параллельны диагоналям исходного четырёхугольника.
или сокращённо
Середины сторон произвольного четырёхугольника — вершины параллелограмма
Доказательство  
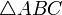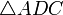Проведём диагональ AC. Отрезки EF и GH будут средними линиями треугольников и . По теореме о средней линии, отрезки будут параллельны диагонали, а, значит, и друг другу. Повторив аналогичные рассуждения для диагонали BD, получаем, что противоположные стороны четырёхугольника EFGH параллельны, и, по определению, это — параллелограм.
Доказательство, что площадь параллелограмма равна половине площади исходного четырехугольника: Пусть диагональ 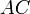проходит внутри четырёхугольника. Тогда площадь треугольник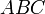а равна 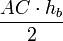, где 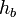--- высота треугольника 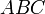, проведённая из вершины 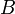. Аналогично, площадь треугольник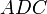а равна 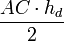. Тогда площадь всего четырёхугольника равна 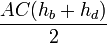. Но 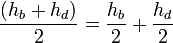— это сумма расстояний до прямой 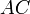от точек 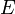и 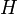, то есть в точности высота параллелограмма 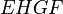. А поскольку сторона 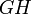параллелограмма вдвое меньше 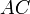, то и площадь параллелограмма равна половине площади ,

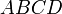Теорема Эйлера

в любом четырехугольнике сумма квадратов сторон равна сумме квадратов диагоналей, сложенной с учетверенным квадратом расстояния между серединами диагоналями


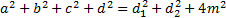
Следствие: Сумма квадратов длин равна  диагоналей параллелограмма равна сумме квадратов длин его сторон

Теорема Птолемея
Для любого выпуклого четырёхугольника ABCD вписанного в окружность, сумма произведений длин противоположных сторон равна произведению длин диагоналей AB*DC+BC*AD=BD*AC
 

Теорема Брахмагупты(площадь вписанного в окружность четырёхугольника)

Если a, b, c, d – длины сторон четырёхугольника, 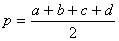 – его полупериметр, а α – сумма его противоположных углов, то площадь Sчетырёхугольника равна
.
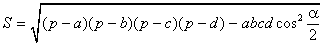В качестве α здесь можно взять сумму любой из двух пар противоположных углов, результат от этого не зависит. В случае четырёхугольника, вписанного в окружность, эта формула принимает более простой вид:
;
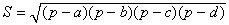это равенство и называется формулой Брахмагупты. Если четырёхугольник имеет и описанную и вписанную окружности, то формула становится совсем короткой: 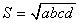.