I.1. Предисловие

Геометрия представляет собой науку о пространственных формах. Греческое слово  означает «землемерие». Геометрия изучает объекты реального мира в наиболее абстрактном виде, отвлекаясь от их конкретного содержания. Абстрактный характер геометрии позволяет широко применять в ней дедуктивный метод, т. е. логическое выведение закономерностей из небольшого числа основных положений (определений и аксиом).

Геометрия возникла из практических задач. Ее приложения выражают реальные факты и находят многочисленные применения. В основе всей техники лежит геометрия, поскольку она появляется всюду, где нужна точность в определении формы и размеров.

Выработка абстрактных геометрических понятий явилась результатом длительного исторического процесса накопления геометрических фактов. Первоначальное установление геометрических фактов происходило экспериментальным путем на огромном числе частных примеров. Правила, полученные в этих частных случаях, обобщались на другие случаи.

В III веке до н. э. в Александрии появилась знаменитая книга – «Начала» Евклида. От латинского названия «Начал» Евклида (Elementa) происходит термин «элементарная геометрия», относящийся к совокупности геометрических результатов. В «Началах» была сделана первая попытка аксиоматического построения курса геометрии. Аксиоматический метод состоит в следующем:

1. Выявляют основные понятия изучаемой геометрии.
2. Все понятия геометрии определяют через основные.
3. Выбирают аксиомы – предложения, принимаемые без доказательства и составляющие основу для доказательства теорем. Список аксиом должен быть таким, чтобы, опираясь на них, можно было получить необходимые выводы.
4. После того, как выделены основные понятия и сформулирован список аксиом, все дальнейшие утверждения (теоремы) выводятся чисто логическим путем.

Мы считаем основными понятиями точку, прямую и плоскость. Прямая и плоскость бесконечны.

1.1. Аксиомы стереометрии

Аксиома 1.1. 

Какова бы ни была плоскость, существуют точки в пространстве, принадлежащие этой плоскости, и точки, не принадлежащие ей.

Аксиома 1.2. 

Если две разные плоскости имеют общую точку, то они имеют и общую прямую, проходящую через эту точку.

Аксиома 1.3. 

Если две разные прямые имеют общую точку, то через них можно провести плоскость, и притом единственную.

Аксиома 1.4. 

Для произвольной плоскости выполняются аксиомы планиметрии.

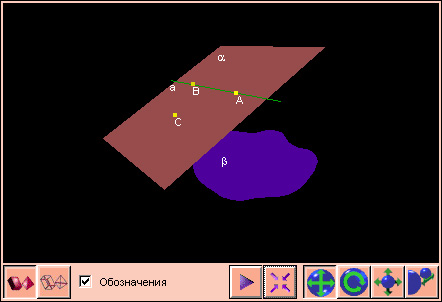
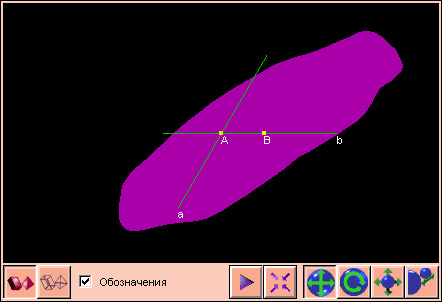
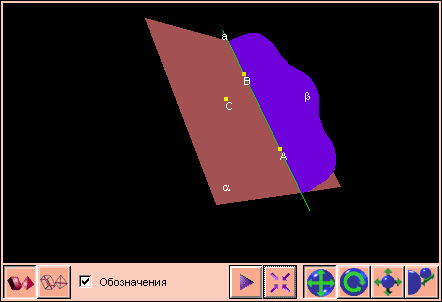
На чертеже 1.1.1 показаны два общепринятых изображения плоскости. Обозначаются плоскости маленькими греческими буквами: α, β, γ, ... Если прямая a лежит в плоскости α, то пишут a  α. Если плоскости α, β пересекаются по прямой l, то пишут α  β  =  l.

1.2. Первые следствия из аксиом стереометрии

Теорема 1.1. 

Через прямую и точку вне ее можно провести плоскость, и притом только одну.

Доказательство

Чертеж 1.2.1. Пусть B  a (чертеж 1.2.1). На прямой a выберем произвольную точку A. Проведем прямую b через точки A и B; a ≠ b, так как B  a. Поаксиоме 1.3  через прямые a и b можно провести плоскость α. Ясно, что a  α и B  α. Докажем от противного, что такая плоскость единственна. Пусть существует плоскость β такая, что a  β, B  β и β ≠ α. Плоскости α и β имеют общую прямую a. Поскольку эти плоскости разные, то все их точки пересечения по аксиоме 1.2 лежат на прямой a. Мы пришли к противоречию, так как точка B, общая для плоскостей α и β, не принадлежит прямой a.

Теорема 1.2. 

Если две точки прямой принадлежат плоскости, то вся прямая принадлежит этой плоскости.

Доказательство

Чертеж 1.2.2. Пусть точки A и B прямой a лежат в плоскости α (чертеж 1.2.2). Возьмем точку C  a. По теореме 1.1 через прямую a и точку C можно провести плоскость β. Если β  =  α, то a  α и теорема доказана. Если β ≠ α, то по аксиоме 1.2 плоскости β и α имеют общую прямую b. Прямые a и b, лежащие в одной плоскости, совпадают, так как имеют две общие точки: A и B. Следовательно, a  α.

Легко доказать следующие теоремы.

Теорема 1.3. 

Плоскость и прямая вне ее либо не имеют общих точек, либо имеют единственную общую точку.

Теорема 1.4. 

Через три точки, не лежащие на одной прямой, можно провести плоскость, и притом только одну.

Сделайте это самостоятельно.