Аксиомы о свойствах плоскости

• Через любые три точки, не принадлежащие одной прямой, можно провести одну и только одну плоскость.
• Две плоскости, которые имеют общую точку, пересекаются по прямой, содержащей эту точку.
• Если плоскости принадлежат две точки прямой, то и вся прямая принадлежит этой плоскости.

Выводы аксиом

• Одну и только одну плоскость можно провести через:
• прямую и точку, не принадлежащую этой прямой;
• две пересекающиеся прямые;
• две параллельные прямые.
• Прямая в пространстве может принадлежать бесконечному множеству плоскостей.

Взаимное положение прямых
Две прямые в пространстве могут пересекаться, скрещиваться и могут быть параллельны.
1. Пересекающиеся прямые
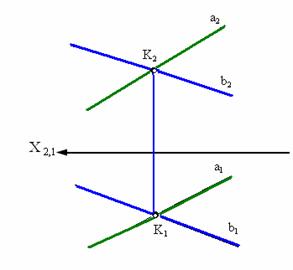
Пересекающимися прямыми называются такие прямые, которые имеют одну общую точку.
Из инвариантного свойства 5 следует, что проекция точки пересечения проекций прямых а и b есть точка пересечения этих прямых (рис. 3.4).
.
Рис. 3.4. Пересекающиеся прямые
2. Параллельные прямые
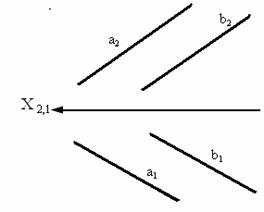
На рис. 3.5 изображены параллельные прямые – прямые, пересекающиеся в несобственной точке (прямые, лежащие в одной плоскости и пересекающиеся в бесконечно удаленной точке).
Из инвариантного свойства 6 следует, что проекции параллельных прямых а и b параллельны.
3. Скрещивающиеся прямые
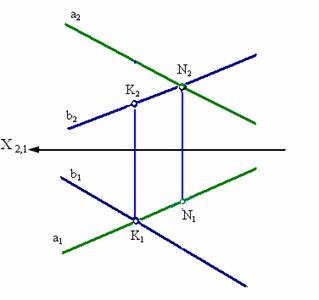
Скрещивающиеся прямые – это прямые, не лежащие в одной плоскости, это прямые не имеющие ни одной общей точки.
На комплексном чертеже (рис. 3.6) точки пересечения проекций этих прямых не лежат на одном перпендикуляре к оси Х (в отличие от пересекающихся прямых, см. рис. 3.4).
.
Рис. 3.5. Изображение параллельных прямых
 .
Рис. 3.6. Скрещивающиеся прямые
Прямая и плоскость в пространство могут:

• а) не иметь общих точек;
• б) иметь ровно одну общую точку;
• в) иметь хотя бы две общие точки.

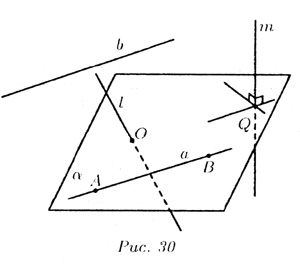
На рис. 30 изображены все эти возможности.
В случае а) прямая b параллельна плоскости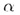: b || .
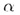В случае б) прямая l пересекает плоскость 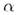в одной точке О; l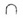 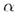= О.
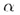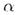
В случае в) прямая а принадлежит плоскости : а или а .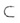
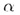Теорема. Если прямая b параллельна хотя бы одной прямой а, принадлежащей плоскости 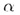, то прямая параллельна плоскости .
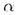Предположим, что прямая m пересекает плоскость 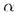в точке Q.Если m перпендикулярна каждой прямой плоскости 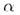, проходящей через точку Q, то прямая m называется перпендикулярной к плоскости .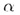