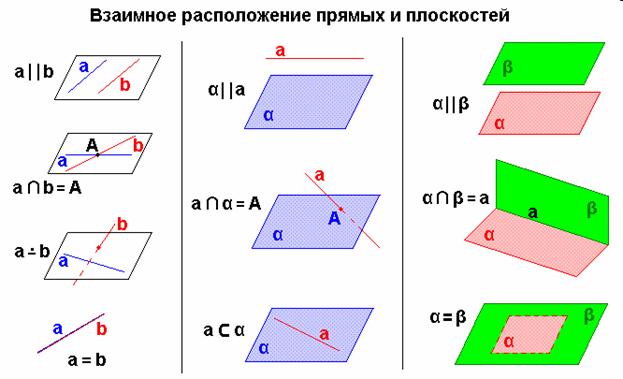
Две плоскости в пространстве могут быть либо параллельны, в частном случае совпадать друг с другом, либо пересекаться. Взаимно перпендикулярные плоскости представляют  собой частный случай пересекающихся плоскостей.
Пусть дается точка К, через которую надо провести плоскость, параллельную некоторой плоскости, заданной пересекающимися прямыми AF и BF (рис. 182).
Очевидно, если через точку К провести прямые СК и DK, соответственно параллельные прямым AF и BF, то плоскость, определяемая прямыми СК и DK, окажется параллельной заданной плоскости.
Другой пример построения дан на рис. 183 справа. Через точку А проведена пл. (3 параллельно пл. ос. Сначала через точку А проведена прямая, заведомо параллельная пл. ос. Это горизонталь с проекциями A"N" и A'N', причем A'N' || hо„. Так
как точка N является фронтальным следом горизонтали AN, то через эту точку пройдет след /{Jр || /а через — след || hga. Плоскости (3 и а взаимно параллельны, так как их одноименные пересекающиеся следы взаимно параллельны.
В"

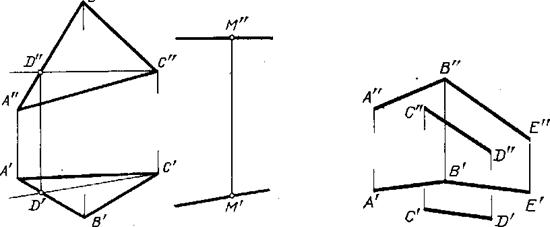
Рис. 181
В"
Рис. 180
Рис. 181

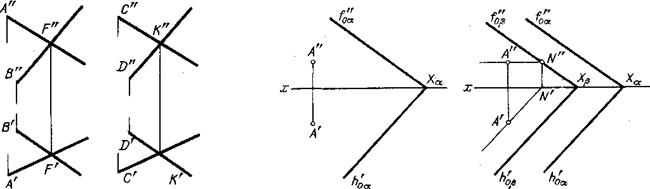
Рис. 182
Рис. 182
Рис. 183
На рис. 184 изображены две параллельные между собой плоскости — одна из них задана треугольником ABC, другая — параллельными прямыми DE и FG. Чем же устанавливается параллельность этих плоскостей? Тем, что в плоскости, заданной прямыми DE и FG, оказалось возможным провести две пересекающиеся

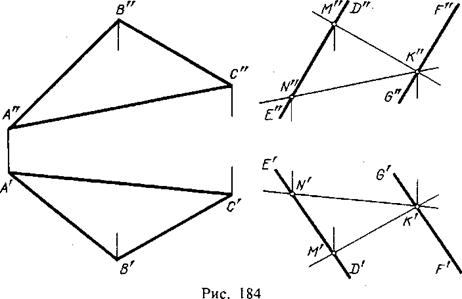
прямые KN и КМ, соответственно параллельные пересекающимся прямым АС и ВС другой плоскости.
Конечно, можно было бы попытаться найти точку пересечения хотя бы прямой DE с плоскостью треугольника ABC. Неудача подтвердила бы параллельность плоскостей.