Прямые в пространстве. Пересекающиеся, параллельные, скрещивающиеся прямые

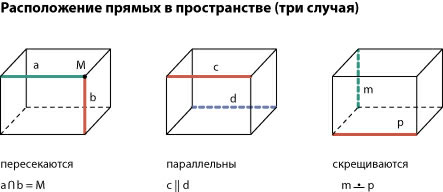
На плоскости две прямые или пересекаются, или параллельны друг другу. А в пространстве возможен еще один случай взаимного расположения прямых.

Две прямые в пространстве параллельны друг другу, пересекаются или скрещиваются.

Если две прямые параллельны третьей, то они параллельны друг другу.

Скрещивающиеся прямые не пересекаются и не параллельны друг другу. Через них невозможно провести плоскость. Скрещивающиеся прямые лежат в параллельных плоскостях.
Углом между двумя скрещивающимися прямыми называется угол между двумя пересекающимися прямыми, соответственно параллельными данным скрещивающимся прямым.

Чертеж 3.1.2.

Определение 3.2.

Перпендикулярность прямой и плоскости

Определение 3.3. 

Прямая называется перпендикулярной плоскости, если она перпендикулярна любой прямой из этой плоскости.

Теорема 3.1. Признак перпендикулярности прямой и плоскости.

Если прямая перпендикулярна каждой из двух пересекающихся прямых плоскости, то она перпендикулярна этой плоскости.

Доказательство

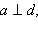Пусть b и c – две пересекающиеся прямые плоскости alpha (чертеж 3.2.1), d – произвольная прямая плоскости alpha, a  b, a  c. Выбираем на этих прямых векторы  как показано на чертеже 3.2.1. Поскольку векторы и  неколлинеарные, то где x и y – некоторые числа. Кроме того, заметим, что так как и Теперь имеем: следовательно, и , а d – произвольная прямая плоскости alpha. Откуда, по определению что и требовалось доказать.

Сформулируем некоторые теоремы, устанавливающие связь между параллельностью и перпендикулярностью в пространстве.

Теорема 3.2. 

Плоскость, перпендикулярная одной из двух параллельных прямых, перпендикулярна и другой.

Теорема 3.3. 

Две прямые, перпендикулярные одной плоскости, параллельны между собой.

Теорема 3.4. 

Если прямая перпендикулярна одной из двух параллельных плоскостей, то она перпендикулярна и другой.

Теорема 3.5. 

Две плоскости, перпендикулярные одной прямой, параллельны между собой.

Докажите эти теоремы самостоятельно, используя такое свойство: если векторы коллинеарные и то

Определение 3.4. 

Перпендикуляром, проведенным из данной точки на данную плоскость, называется отрезок прямой, перпендикулярной данной плоскости, который соединяет данную точку с точкой плоскости.

Пусть AO – перпендикуляр к плоскости alpha (чертеж 3.2.4), O – основание перпендикуляра. Длина этого перпендикуляра AO называется расстоянием от точки A до плоскости alpha. Отрезок, соединяющий точку A с любой точкой плоскости, отличной от O, называется наклонной (AB – наклонная, B – основание наклонной, BO – проекция наклонной на плоскость alpha, то есть BO = Пр_alphaAB).

Теорема 3.6. 

Если из одной точки вне плоскости проведены к ней перпендикуляр и наклонные, то

• длина перпендикуляра меньше длины любой наклонной;
• наклонные с равными проекциями равны;
• из двух наклонных большую длину имеет та, у которой больше проекция.

Теорема 3.7. О трех перпендикулярах.

Для того, чтобы прямая на плоскости была перпендикулярна наклонной, необходимо и достаточно, чтобы эта прямая была перпендикулярна ортогональной проекции наклонной на плоскость.

Необходимость. Пусть b  alpha и b  AB (чертеж 3.2.5). Поскольку b  AO, так как AO  alpha, то b  AOB по признаку взаимной перпендикулярности прямой и плоскости; следовательно, b  OB.

Достаточность. Пусть b  alpha и b  OB. Учитывая, что b  AO, имеем b перепендикулярна плоскости AOB; следовательно, b  AB.

Две прямые в пространстве называются перпендикулярными, если они образуют прямой угол. На чертеже 3.1.2 изображен куб ABCDA1B1C1D1. Скрещивающиеся прямые A1D1 и CD перпендикулярны. Действительно, A1D1 C1D1, а C1D1 || CD.

Назовем еще несколько пар скрещивающихся перпендикулярных прямых: A1D1 и AB, A1B1 и BC, A1B1 и AD, B1C1 и AB.

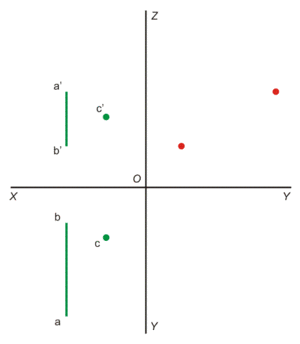
Дано.
Прямая АВ и точка С.
Требуется.
Провести через точку С плоскость Р, перпендикулярную к прямой АВ.
Решение.
Поскольку и горизонтальная и вертикальная проекции прямой АВ перпендикулярны оси проекций ОХ, любая плоскость со следами перпендикулярными осям OZ и OY (или параллельная оси ОХ) будет перпендикулярна прямой АВ.
Для решения задачи надо только соблюсти перпендикулярность в профильной плоскости.
Поэтому сначала строим профильные проекции прямой АВ и точки С. Затем из профильной проекции точки С опускаем перпендикуляр на профильную проекцию прямой АВ и продлеваем его до пересечения с осями OZ и OY. Получается профильный след PW искомой плоскости.
Достраиваем вертикальный PV и горизонтальный PH следы этой плоскости.