Угол между плоскостями. Перпендикулярность плоскостей
Пусть плоскости alpha и beta пересекаются по прямой с.
Угол между плоскостями — это угол между перпендикулярами к линии их пересечения, проведенными в этих плоскостях.
Другими словами, в плоскости alpha мы провели прямую а, перпендикулярную с. В плоскости beta — прямую b, также перпендикулярную с. Угол между плоскостями alpha и beta равен углу между прямыми а и b.
Заметим, что при пересечении двух плоскостей вообще-то образуются четыре угла. Видите их на рисунке? В качестве угла между плоскостями мы берем острый угол.
Если угол между плоскостями равен 90 градусов, то плоскости перпендикулярны,
Это определение перпендикулярности плоскостей. Решая задачи по стереометрии, мы используем также признак перпендикулярности плоскостей:
Если плоскость alpha проходит через перпендикуляр к плоскости beta, то плоскости alpha и beta перпендикулярны.
Перпендикулярность двух плоскостей
Определение 3.5.
Пусть прямая a является линией пересечения плоскостей alpha и beta (чертеж 3.3.1). Пусть плоскость gamma, перпендикулярная прямой a, пересекает плоскости alpha и beta по прямым m и n, которые взаимно перпендикулярны, то есть gamma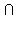 
alpha = m, gamma 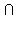beta = n и m 
n. Такие плоскости alpha и beta называются взаимно перпендикулярными.
Это определение не зависит от плоскости gamma. Действительно, если провести другую плоскость δ, перпендикулярную прямой a, то δ || gamma.
Пусть δ 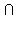alpha = m', δ 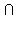beta = n'. По теореме о следах m' || m и n' || n. Угол, образованный прямыми m' и n', и угол, образованный прямыми m и n, равны как углы с соответственно параллельными и одинаково направленными сторонами.
Теорема 3.8. Признак перпендикулярности двух плоскостей.
Пусть a alpha, a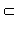 
beta, тогда beta alpha. То есть, если плоскость beta содержит прямую a, перпендикулярную плоскости alpha, то плоскости alpha и beta перпендикулярны.
Доказательство
Пусть a alpha, a beta и alpha beta = b (чертеж 3.3.2), c – прямая, лежащая в плоскости alpha и проходящая через точку O пересечения прямой a с плоскостью alpha и с b. Через прямые a и c проведем плоскость gamma. Имеем gamma b, так как a b и c b. Поскольку a c, то по определению beta alpha
Теорема 3.9.
Пусть alpha beta, alpha 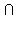beta = a, b a, b 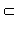beta, тогда b alpha. То есть прямая b, лежащая в одной из взаимно перпендикулярных плоскостей beta и перпендикулярная линии пересечения a этих плоскостей, перпендикулярна и другой плоскости alpha.
Доказательство
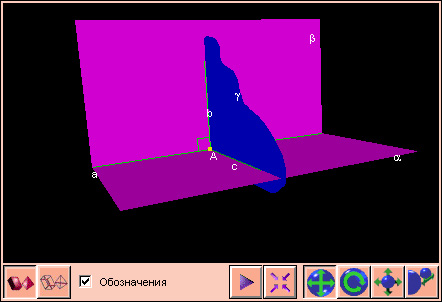
Пусть b 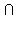a = A (чертеж 3.3.3), a = alpha 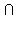beta и beta alpha. В плоскости alpha проведем прямую c через точку A перпендикулярно прямой a. Проведем плоскость gamma через прямые b и c. Имеем gamma a по признаку перпендикулярности прямой и плоскости. Поскольку alpha beta, то b c, следовательно, b a и b c, откуда следует, что b alpha.
Теорема 3.10.
Если плоскости alpha и beta взаимно перпендикулярны, и к плоскости alpha проведен перпендикуляр, имеющий общую точку с плоскостью beta, то этот перпендикуляр лежит в плоскости beta.
Теорема 3.11.
Пусть плоскости alpha и beta перпендикулярны плоскости gamma и пересекаются по прямой a, тогда a gamma.
Доказательство
На прямой a выберем произвольную точку A (чертеж 3.3.4). Проведем через точку A перпендикуляр к плоскости gamma. По теореме 3.9 этот перпендикуляр лежит в каждой из плоскостей alpha, beta, следовательно, он лежит на линии их пересечения.
