
Угол между скрещивающимися прямыми и расстояние между ними.
Расстояние от точки до плоскости и от прямой до параллельной ей плоскости
Скрещивающиеся прямые не параллельны и не пересекаются. Они лежат в параллельных плоскостях, и поместить их в одну плоскость невозможно.

Часто в задачах требуется найти угол между скрещивающимися прямыми. Как это сделать?
Угол между прямыми, лежащими в одной плоскости, найти нетрудно. Можно измерить его транспортиром. Можно найти из какого-нибудь треугольника по теореме синусов или косинусов.
Пусть скрещивающиеся прямые a и b лежат в параллельных плоскостях α и β. Проведем в плоскости β прямую с, параллельную прямой а. Угол между прямыми а и b равен углу между прямыми b и с.
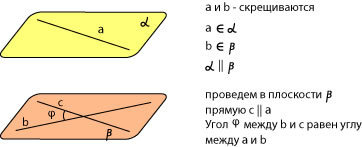
Можно сказать, что угол между скрещивающимися прямыми — это угол между параллельными им прямыми, лежащими в одной плоскости.
Расстояние между скрещивающимися прямыми равно длине их общего перпендикуляра.
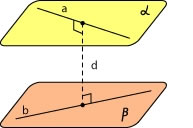
Другими словами, расстояние между скрещивающимися прямыми равно расстоянию между параллельными плоскостями, в которых они лежат.
Дадим еще два полезных определения.
Расстояние от точки до плоскости — это длина перпендикуляра, опущенного из точки на плоскость.
Расстояние от прямой до параллельной ей плоскости — длина перпендикуляра, опущенного на плоскость из любой точки этой прямой.
Заметим, что расстояние от точки до плоскости или угол между скрещивающимися прямыми иногда проще найти с помощью координатно-векторного метода.
Определение 3.6.
Общим перпендикуляром двух скрещивающихся прямых называется отрезок с концами на этих прямых, перпендикулярный каждой из этих прямых.
Теорема 3.12.
Две скрещивающиеся прямые имеют общий перпендикуляр, и притом единственный.
Доказательство
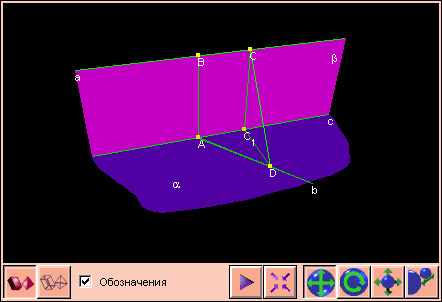
Пусть ![]() beta = c
beta = c![]() b = A
b = A![]() alpha
alpha![]() b
b![]() a
a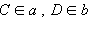 ),
), 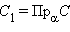 . Поскольку
. Поскольку  и
и 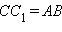 . Кроме того,
. Кроме того, 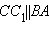 , следовательно,
, следовательно, 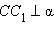 . Видно, что
. Видно, что  , то есть
, то есть
Лемма 3.1.
Две скрещивающиеся прямые лежат в параллельных плоскостях.
Доказательство
Пусть 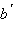 и
и 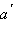 соответственно такие, что
соответственно такие, что 
 Образуется две пары пересекающихся прямых параллельных прямым другой пары. По признаку параллельности плоскостей эти пары прямых определяют две параллельные плоскости, в которых и лежат данные скрещивающиеся прямые.
Образуется две пары пересекающихся прямых параллельных прямым другой пары. По признаку параллельности плоскостей эти пары прямых определяют две параллельные плоскости, в которых и лежат данные скрещивающиеся прямые.