Ортотреугольник.
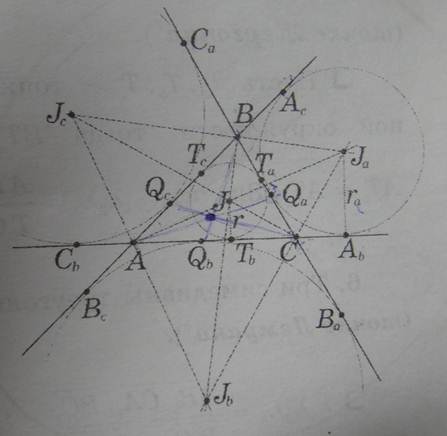
Рассмотрим треугольник 
.
В нем 
– высоты, так как биссектриса внутреннего угла
всегда перпендикулярна биссектрисе внешнего угла.
Таким образом, треугольник ABC
образован основаниями высот треугольника 
.
Такой треугольник называют ортоцентрическим ( или ортотреугольником).
Теорема.
Ортоцентр остроугольного треугольника ABC
является центром окружности, вписанной в его ортотреугольник A1B1C1
Док-во:
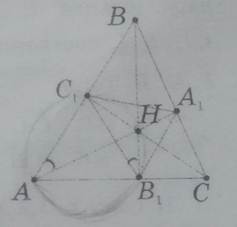
Около четырехугольника 
можно описать окружность, так как <
+<
= π.
Тогда <
= <
.
Аналогично, <
= <
C другой стороны, треугольник 
~ треугольнику 
,
Значит , < = <.
Таким образом, < = <,
то есть, 
– биссектриса угла 
.
Аналогично доказываем, что 
и 
также биссектрисы. Следовательно, точка H – центр вписанной в
треугольник A1B1C1 окружности.
Доказано.
Замечания:
1)
Если треугольник ФИС прямоугольный, то
ортотреугольник вырождается в высоту, проведенную к гипотенузе;
2)
Если треугольник ABC тупоугольный,
то его ортоцентр является центром вневписанной окружности ортотреугольника.
ХЗ ЧО ЗА РАДИУС ВЕКТОР
И ТЕОРЕМА О ТОЧКАХ!!
