Симедиана – это чевиана треугольника, симметричная медиане относительно биссектрисы, проведенной из той же вершины.
Свойства:
- Отрезки, на которые симедиана делит противоположную сторону, пропорциональны квадратам прилежащих сторон.

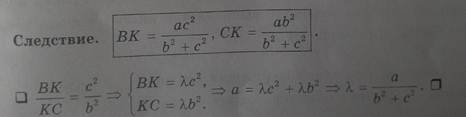
- Симедианы треугольника пересекаются в одной точке, которая называется точкой Лемуана ( обозначается K или L.)
- Сумма квадратов расстояний от точки на плоскости до сторон треугольника минимальна, когда эта точка является точкой Лемуана.
- Расстояния от точки Лемуана до сторон треугольника пропорциональны длинам сторон.
- Точка Лемуана — единственная точка, которая является центроидом своего педального (Тангенциальный )треугольника.
Длина симедианы равна: 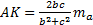
Тангенциальный треугольник  точки относительно
точки относительно 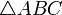 . Треугольник, вершинами которого являются основания перпендикуляров, опущенных из точки
. Треугольник, вершинами которого являются основания перпендикуляров, опущенных из точки 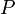 на стороны треугольника
на стороны треугольника 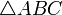 (или их продолжения).
(или их продолжения).

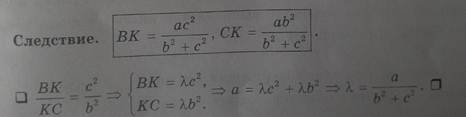

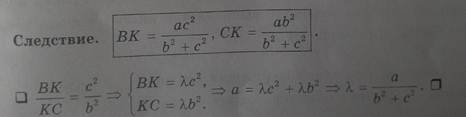
![]()
![]() точки относительно
точки относительно ![]() . Треугольник, вершинами которого являются основания перпендикуляров, опущенных из точки
. Треугольник, вершинами которого являются основания перпендикуляров, опущенных из точки ![]() на стороны треугольника
на стороны треугольника ![]() (или их продолжения).
(или их продолжения).