Треугольник, полученный соединением середин сторон данного
треугольника, назовем серединным треугольником. На рисунке 15
треугольник A′B′C′ есть серединный треугольник треугольника
ABC. Рассмотрим также две медианы AA′ и BB′,
пересекающиеся в точке O, две высоты треугольника ABC,
пересекающиеся в точке H, и две высоты треугольника
A′B′C′, пересекающиеся в точке O

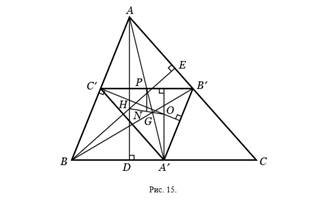
Во-первых, стороны треугольника A′B′C′ параллельны сторонам
треугольника ABC, поэтому эти треугольники подобны. Далее,
отношение длин любых двух соответствующих отрезков (а не только
соответствующих сторон) будет равно 1 : 2, В действительности, отрезки
B′C′, C′A′, A′B′ разбивают треугольник ABC
на четыре конгруэнтных треугольника. Кстати, точка P — середина
отрезка B′C′ — также является и серединой отрезка AA′.

Далее мы видим, что AC′A′B′ — параллелограмм, следовательно,
прямая AA′ делит пополам отрезок B′C′, Поэтому медианы
треугольника A′B′C′ лежат на медианах треугольника ABC, а
это означает, что оба треугольника имеют один и тот же
центроид G.

Высоты треугольника A′B′C′, изображенные нами на рисунке,
являются серединными перпендикулярами сторон AB и BC
треугольника ABC. Отсюда мы делаем вывод, что точка O —
ортоцентр треугольника A′B′C′ — является в то же время и центром
окружности, описанной вокруг треугольника ABC.

Так как точка H — ортоцентр треугольника ABC, а точка
O — ортоцентр подобного ему треугольника A′B′C′, то
|AH| = 2 |OA′|. Вспомним, что по теореме 1.32
|AG| = 2 |GA′|. И наконец, так как оба отрезка, AD
и OA′, перпендикулярны стороне BC, то они параллельны.
Следовательно,

HAG^=OA′G^,
?HAG ? ?OA′G,
и
AGH^=A′GO^
.

Этим показано, что точки O, G, H коллинеарны *) и
|HG| = 2 |GO′|

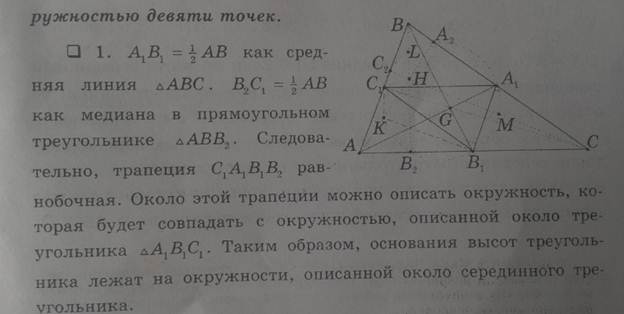
Теорма.  Середины K, L,M отрезков AH, BH, CH, соединяющих вершины треугольника с ортоцентром , основания медиан A1,B1,C1 и высот A2,B2,C2 лежат на одной окружности. (окружность эйлера, окружность девяти точек)