Оптимальное кодирование

{Код шеннона внизу}

Одно и то же сообщение можно закодировать различными способами. Оптимально закодированным будем считать такой код, при котором на передачу сообщений затрачивается минимальное время. Если на передачу каждого элементарного символа (0 или 1) тратиться одно и то же время, то оптимальным будет такой код, который будет иметь минимально возможную длину.

Пример 1.

Пусть имеется случайная величина  X(x₁,x₂,x₃,x₄,x₅,x₆,x₇,x₈), имеющая восемь состояний  с распределением вероятностей

Для кодирования алфавита из восьми букв без учета вероятностей равномерным двоичным кодом нам понадобятся три символа:

   Это         000, 001, 010, 011, 100, 101, 110, 111

Чтобы ответить, хорош этот код или нет, необходимо сравнить его с оптимальным значением, то есть определить энтропию

Определив избыточность L по формуле L=1-H/H₀=1-2,75/3=0,084,  видим, что возможно сокращение длины кода  на 8,4%.

Возникает вопрос: возможно ли составить код, в котором на одну букву будет, в среднем приходится меньше элементарных символов.

Такие коды существуют. Это коды Шеннона-Фано и Хаффмана.

Принцип построения оптимальных кодов:

1.   Каждый элементарный символ должен переносить максимальное количество информации, для этого необходимо, чтобы элементарные символы (0 и 1) в закодированном тексте встречались в среднем одинаково часто. Энтропия в этом случае будет максимальной.

2.   Необходимо буквам первичного алфавита, имеющим большую вероятность, присваивать более короткие кодовые слова вторичного алфавита.

Код Шеннона-Фано

Пример 2. Закодируем буквы алфавита из примера 1 в коде Шеннона-Фано.

Все буквы записываются в порядке убывания их вероятностей, затем делятся на равновероятные группы, которые обозначаются 0 и 1, затем вновь делятся на равновероятные группы и т.д. (см.табл.4.1)

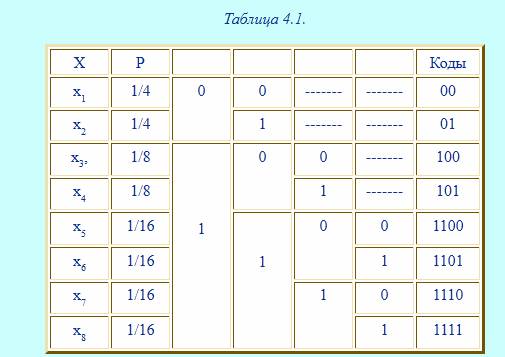
Средняя длина полученного кода будет равна

Итак, мы получили оптимальный код. Длина этого кода совпала с энтропией. Данный код оказался удачным, так как величины вероятностей точно делились на равновероятные группы. 

Пример 3{этот пример необязателен к списыванию, так для общего развития(прим.автор)} .

Возьмем 32 две буквы русского алфавита. Частоты этих букв известны. В алфавит включен и пробел, частота которого составляет 0,145. Метод кодирования представлен в таблице 4.2.

 Средняя длина данного кода будет равна,  бит/букву;

Энтропия  H=4.42 бит/буква.  Эффективность полученного кода можно определить как отношение энтропии к средней длине кода. Она равна 0,994. При значении равном единице код является оптимальным. Если бы мы кодировали кодом равномерной длины , то эффективность была бы значительно ниже.